Geeking Out About Card Deck Distributions Again


A few weeks ago, I was geeking out about multi-triangular deck distributions and noted that I was a little bugged that I didn't go through every possible combinatorial permutation of triangular decks ranked 1-4. Well, here it is, and there are some curious findings.

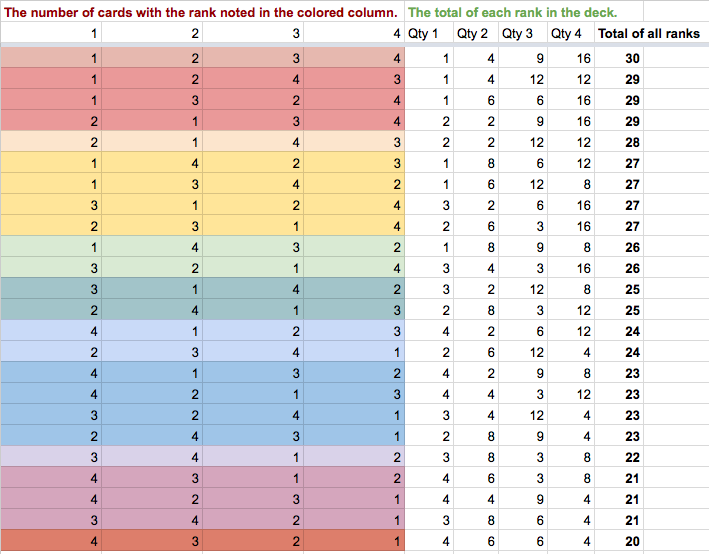
Let me back up a bit. This spreadsheet outlines several "triangle" decks, which are typically a deck of cards in which each card is ranked with a number. That number is also how frequent that card is in the deck. So there are one 1, two 2s, three 3s, four 4s in the deck. The top row of numbers is the frequency, the colored rows below that are the ranks. A typical 1-4 triangle deck is noted on the first colored row.

The white section to the right is the sum of all ranks. First, multiplying their frequency by their rank, then totalling up all those products into one grand total.

Now, why would this be useful? In my case, I wanted to figure out a resource deck for Monsoon Market. I wanted each resource to only occupy ten cards in the deck, but their ranks to be distributed in a somewhat triangular fashion, to vary their overall rarity.

So for example, if I wanted a very common resource, I'd assign it the distribution noted on the top row (1x1, 2x2, 3x3, 4x4), which is a total of 30 of that resource. On the flipside, if I wanted a very rare resource, I'd assign it the very last row's distribution (1x4, 2x3, 3x2, 4x1). And there is a nice spectrum in between. In my case, I like the even totals: 30, 28, 26, 24, 22, 20.

Now it's very easy to get lost in the weeds with this kind of obsession. I guarantee you that no one but the most die hard card-counter will bother calculating these totals. In fact, I could just as easily make every resource follow a standard triangle distribution just to make it easier for everybody to figure out. And I might! But this kind of fiddling is still good to have done at least once.

Comments

Post a Comment

Popular posts from this blog

5 Graphic Design and Typography Tips for your Card Game

Image
Chris Farrell of Illuminating Games just wrote a thorough critique of card games setting their body text to be so small that they cannot be read at arm's length, let alone across the table. Here's an excerpt, but the whole thing is worth a read for any would-be card game designers out there. (Myself included.) Break out your copy of the base set of Dominion, and look at the Chapel. This has a text box roughly 3.5cm by 4.5cm. It's got a single line of text. That line of text is 1 (one) millimeter high. 1mm! For me, it's only clearly readable at half an arm's length even in the bright light of day. (...) Compare this to a more sane game like Glory to Rome, where the font size is 2-3 times as large (text is 2mm high, keywords 3mm and usually highlighted). I can generally read Glory to Rome cards across the table, and can certainly see the important keywords. To heap insult upon injury, not only does Glory to Rome have far more legible text than Dominion it also has...
Read more

Low-High Dice Game

Image
A dice game inspired by the stock market (and playing lots of Martian Dice). Roll a bunch of dice and choose which sets to keep. Choose your strategy wisely! Stuff You Need Two-to-Six PLAYERS A PENCIL and PAPER to keep score Thirteen standard six-sided DICE How to Play The shortest player takes the first turn. On your turn, first roll all thirteen dice. Several dice will have matching results. These are called SETS. (A single die result is a set, too.) You must choose a set to keep. For example, your first roll results are 111124445555 . The sets are four 1 s, one 2 , three 4 s, and four 5 s. After keeping a set of dice, lock them up in a row. This is called the GOOD TRACK. For example,  you could keep the set of four 1 s, one 2 , three 4 s, or four 5 s . You decide to keep the four 1 s and line them up in your good track. After keeping a set, you may end your turn or re-roll the remaining unlocked dice. When you re-roll, immediately set aside any results tha...
Read more

The Thousand-Year Game Design Challenge

Image
UPDATE: The submission period has closed and here are the entries. If you're an entrant, continue sending pics or vids of people playing your game. The first step to a game lasting a thousand years is for people to play it today. UPDATE 2: And here's the winner! To support games designed for longevity – that can be learned, played and shared for hundreds of years – we offer this challenge to any game designers, artists and imaginative people who also share this desire. Challenge Create a game. The game can be of any theme or genre you desire, but there is one restriction: You're creating a "new classic," like Chess, Tag or card games. So, create a game to be enjoyed by generations of players for a thousand years. Prize $1,000 to the winning entrant, to be announced and awarded January 1, 2012. Entry Deadline Entries must be submitted before midnight July August 31st, 2011. ( Update ) Entry Guidelines Enter by posting a comment below with a link ...
Read more